Home >> PURE MATHS, Sequences & Series, arithmetic series

Arithmetical Series Structure

An arithmetical series starts with the first term, usually given the letter 'a'.

For each subsequent term of the series another term is added. This is a multiple of the letter 'd' called 'the common difference'.

So the series has the structure:

where S_nis the sum to 'n' terms, the letter 'l' is the last term.

The common difference 'd' is calculated by subtracting any term from the subsequent term.

The nth term(sometimes called the 'general term' is given by:

back to top

Proof of the Sum of an Arithmetical Series

The sum of an arithmetical series is found by adding two identical series together, but putting the second series in reverse order.

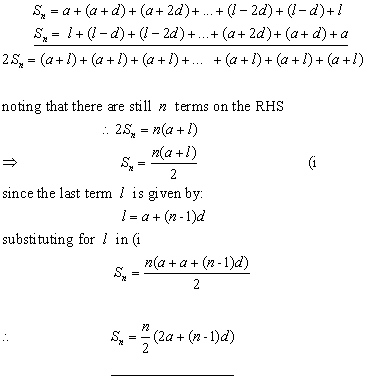
Example #1

In an arithmetical progression the 8th term is 23 and the 11th term is 4 times the 3rd term.

Find the 1st term, the common difference and the sum of the first 10 terms.

back to top

Example #2

The sum of terms of an arithmetic progression is 48.

If the first term is 3 and the common difference is 2, find the number of terms.

back to top

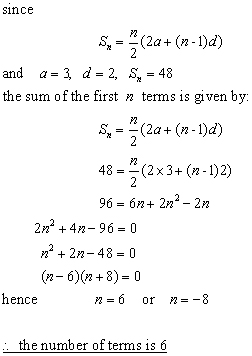
Arithmetic Mean

This is a method of finding a term sandwiched between two other terms.

The required term is calculated by taking an average of the term before and the term after.

So if we have a sequence of terms: a b c and a and c are known. Then term b is given by:

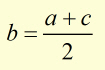
Example

If the 3rd term of an arithmetical progression is 7 and the 5th term is 11, what is the 4th term?

Let the 3rd term be 'a' and the 5th term 'c'.

Then the 4th term 'b' is given by:

back to top

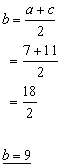
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]