Home >> PURE MATHS, Algebra, inequalities
first principles |
Symbols
x greater than y
x less than y
x greater than or equal to y
x less than or equal to y
The Rules of Inequalities (sometimes called 'inequations')
These are the same as for equations i.e that whatever you do to one side of the equation(add/subtract, multiply/divide by quantities) you must do to the other.
However, their are two exceptions to these rules.
When you multiply each side by a negative quantity .
'<' becomes '>', or '>' becomes '<'
That is, the inequality sign is reversed.
Similarly, when you divide each side by a negative quantity .
< becomes >, or > becomes<
As before, the inequality sign is reversed.
example #1
solve for x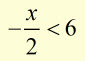 
multiplying each side by -2
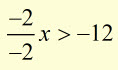
note how the inequality sign changes: < to >
example #2
solve for x 
dividing each side by -5
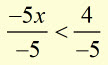
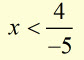
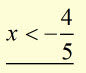
Inequalities with ONE variable
Example #1 - Find all the integral values of x where,
The values of x lie equal to and less than 6 but greater than -5, but not equal to it.
The integral(whole numbers + or - or zero) values of x are therefore:
6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4
Example #2 - What is the range of values of x where,
Since the square root of 144 is +12 or -12(remember two negatives multiplied make a positive), x can have values between 12 and -12.
In other words the value of x is less than or equal to 12 and more than or equal to -12. This is written:
Inequalities with TWO variables - Solution is by arranging the equation into the form:
Then, above the line of the equation,
and below the line,
Consider the graph of 
note - the first term A must be made positive by multiplying the whole equation by -1
hence 
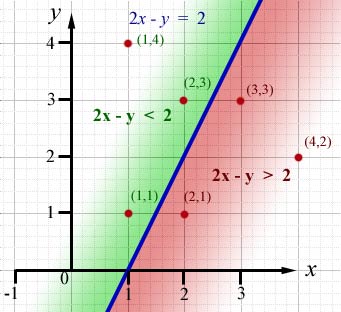
Look at the points(red) and the value of 2x - y for each.
(The blue line is the graph of the equation rearranged as y = 2x - 2 )
The table below summarises the result.
|
point(x,y) |
2x - y |
value |
more than 2 ? |
above/below |
(1,1) |
2(1)-(1) |
1 |
no - less |
above |
(1,4) |
2(1)-(4) |
-2 |
no - less |
above |
(2,3) |
2(2)-(3) |
1 |
no - less |
above |
(3,3) |
2(3)-(3) |
3 |
yes - more |
below |
(2,1) |
2(2)-(1) |
3 |
yes - more |
below |
(4,2) |
2(4)-(2) |
6 |
yes - more |
below |
The Modulus
The modulus is the numerical value of a number, irrespective of the sign it carries.
hence l x l < 3 means -3 < x < 3
Example
solve for x 
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]