Home >> MECHANICS, Momentum & Impulse, conservation of linear momentum
conservation law |
The Principle of Conservation of Momentum
The total linear momentum of a system of colliding bodies, with no external forces acting, remains constant.
For two perfectly elastic colliding bodies note:
i) By Newton's 3rd. Law,
the force on X due to Y , (Fx) ............... is the same as the force on Y due to X , (Fy) .
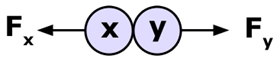
Fx = Fy
ii) By Newton's 2nd. Law, the rate of change of momentum is the same, since F = (rate of change of momentum)
iii) Because the directions of the momentum of the objects are opposite, (and therefore of different sign) the net change in momentum is zero.
Example #1
A 5 kg mass moves at a speed of 3 ms-1 when it collides head on, with a 3 kg mass travelling at 4 ms-1, travelling along the same line.
After the collision, the two masses move off together with a common speed.
What is the common speed of the combined masses?

Example #2
An artillery shell of mass 10 kg is fired from a field gun of mass 2000 kg.
If the speed of the shell on leaving the muzzle of the gun is 250 ms-1 , what is the recoil speed of the gun?

Energy changes during collisions
Consider the kinetic energy change involved during a collision. Remember that no energy is actually lost, it is just converted into other forms.
Energy can be transformed into heat, sound and permanent material distortion. The later causes the internal potential energy of bodies to increase.
If no kinetice energy is lost (K.E.= ½ mv2 ) then the collision is said to be perfectly elastic.
However if kinetic energy is lost, the collision is described as inelastic.
In the special case when all the kinetic energy is lost, the collision is described as completely inelastic. This is when to two colliding bodies stick to one another on impact and have zero combined velocity.
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
