Home >>STATISTICS, Section 1, discrete random variables 4
defn. Discrete Uniform Distribution |
Revision
A continuous random variable can have any value between two specified values.
eg x = 3.14 from 2 < x < 4
A discrete random variable has only one value chosen from a list of exact values.
eg x = 7 from 3, 4, 5, 6, 7, 8, 9
Definition of a Discrete Uniform Distribution
This is a probability distribution where a number of equally spaced values are equally likely to happen.
If there are n values each has an equal probability 1/n of occuring.
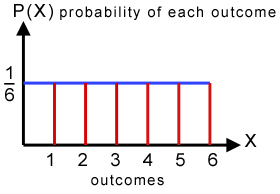
Take the example of throwing a fair die. The graph below describes the distribution of probabilities.
The appearance is a straight line. Each probability for each event is the same.
In mathematical terms, a discrete normal distribution is a set of n integer values.
Values vary incrementally from the lowest value, a to the highest value, b.*
a, a+1, a+2, a+3, . . . . b-3, b-2, b-1, b
*note a and b are both integers, where a < b
The number of values is b - a + 1 .
To make this clear, think of a series that starts with a = 3 and ends with b = 11 .
Since each value is incremented by '1' , the number of values is ( 11 - 3 + 1 = 9 )
3 4 5 6 7 8 9 10 11
So the probability P(X = x) of each value occuring 1/n , is given by:
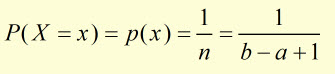
Derivation of Expected Value (for discrete uniform distribution)
Generally, the expected value is given by:
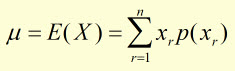
but p(xr) is the same for each vale, that is 1/n , hence:
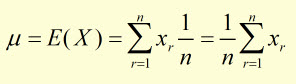
The expression ![]() is the sum(S) of an arithmetic progression, with the first term a ,
is the sum(S) of an arithmetic progression, with the first term a ,
last term is b a common difference of '1' and n terms.
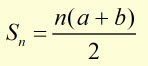
hence,
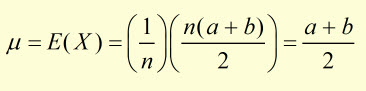
In the example of tossing a fair die*, a = 1 and b = n .
*or any situation where the outcomes are consecutive numbers starting with 1
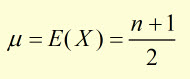
Derivation of Variance (for discrete uniform distribution)*
*simplified case with a = 1 and b = n
Variance is found from the expected value expression:
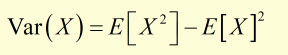
We already have E(X) from above. So E(X)2 is given by:
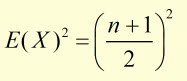
E(X)2 is found from:
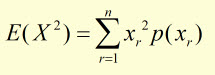
This simplifies to:
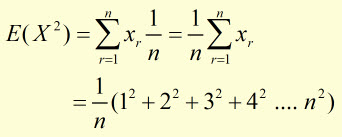
The sum Sn of a series of n squared numbers is given by:
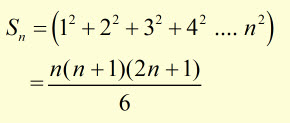
therefore,
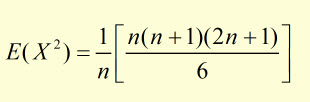
cancelling the n's
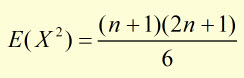
substituting for E(X2)and E(X)2 into the Var(X) equation:
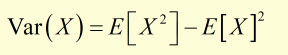
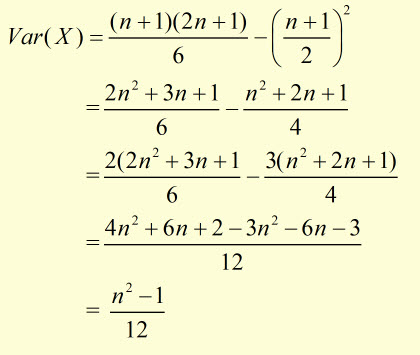
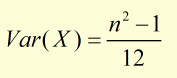
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
