Home >> PURE MATHS, Algebra, partial fractions
Definitions |
Some Definitions:
Proper Fraction
When the degree(index) of the function is higher in the denominator than the numerator.
Improper Fraction
When the degree(index) of the function is higher in the numerator than the denominator.
Partial Fractions
Factorising the denominator of a proper fraction means that the fraction can be expressed as the sum(or difference) of other proper fractions.
Simple Addition/Subtraction of Algebraic Fractions
As with simple fraction arithmetic, a common denominator is found from the denominators of either fraction.
The numerators are subsequently altered to be fractions of the new denominator.
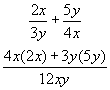
![]()
Equations & Identities
Equations are satisfied by discrete values of the variable involved.
Example:
![]()
Identities are satisfied by any value of the variable used.
Note the equals sign '=' is modified to reflect this.
Example:
![]()
When we make partial fractions(below) we are creating an identity from the original expression.
Denominator with only 'Linear Factors'
By 'linear' we mean that x has a power no higher than '1' . In other words, this method does not work with x2, x3, x4 etc.
For each linear factor of the type:
![]()
there is a partial fraction:
![]()
hence:
![]()
where x is a variable and A,B,a,b,c,d are constants, where 'a' is not equal to 'b'.
Example #1
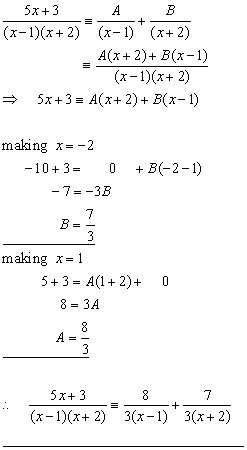
Denominator with 'Repeated Linear Factors
For each 'repeated' linear factor of the type:
![]()
there is a partial fraction:
![]()
hence:
![]()
where x is a variable and A,B,C,a,b,c,d are constants, where 'a' is not equal to 'b'.
Example #1

Denominator with a Quadratic Factor
For each quadratic factor of the type:
![]()
there is a partial fraction:
![]()
hence:
![]()
Example #1
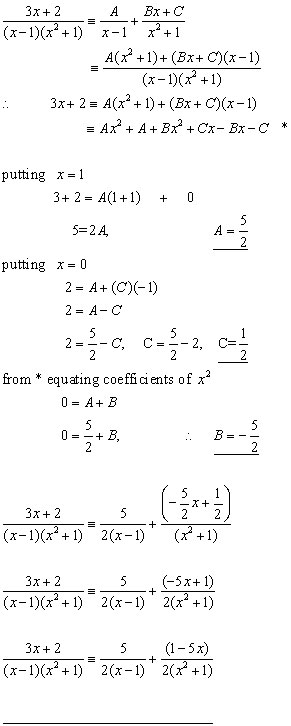
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
